在分布式系统中,一个核心挑战是如何 将数据均匀分布到多个服务器上,并且在系统扩容或缩容时,尽量减少数据迁移。
一致性哈希(Consistent Hashing) 算法就是为了解决这个问题而提出的,它在缓存系统、负载均衡、分布式存储(如 Cassandra、Amazon Dynamo)中都有广泛应用。
传统哈希的局限性
设想这样一个场景:我们有 4 台缓存服务器 S1、S2、S3、S4,需要存储大量键值对。
一种常见的方式是对 key 取哈希值,然后用取模运算来决定放在哪台服务器上:
server = hash(key) % N
其中 N 是服务器数量。
这种方法虽然简单,但有一个致命问题: 当服务器数量变化时,几乎所有数据都需要重新分布。
比如,当我们从 4 台扩容到 5 台服务器时:
原映射: server = hash(key) % 4
新映射: server = hash(key) % 5
几乎所有 key 的哈希值都会对应到新的服务器上,造成大量缓存失效和数据迁移。这在大规模系统中是不可接受的。
一致性哈希的核心思想
一致性哈希通过引入 哈希环(Hash Ring),巧妙地解决了这个问题。
- 哈希环的构建
一致性哈希将整个哈希空间(比如 0 到 2³²-1)首尾相连,形成一个 环形结构:
0 → 1 → 2 → ... → 2³²-1 → 回到 0
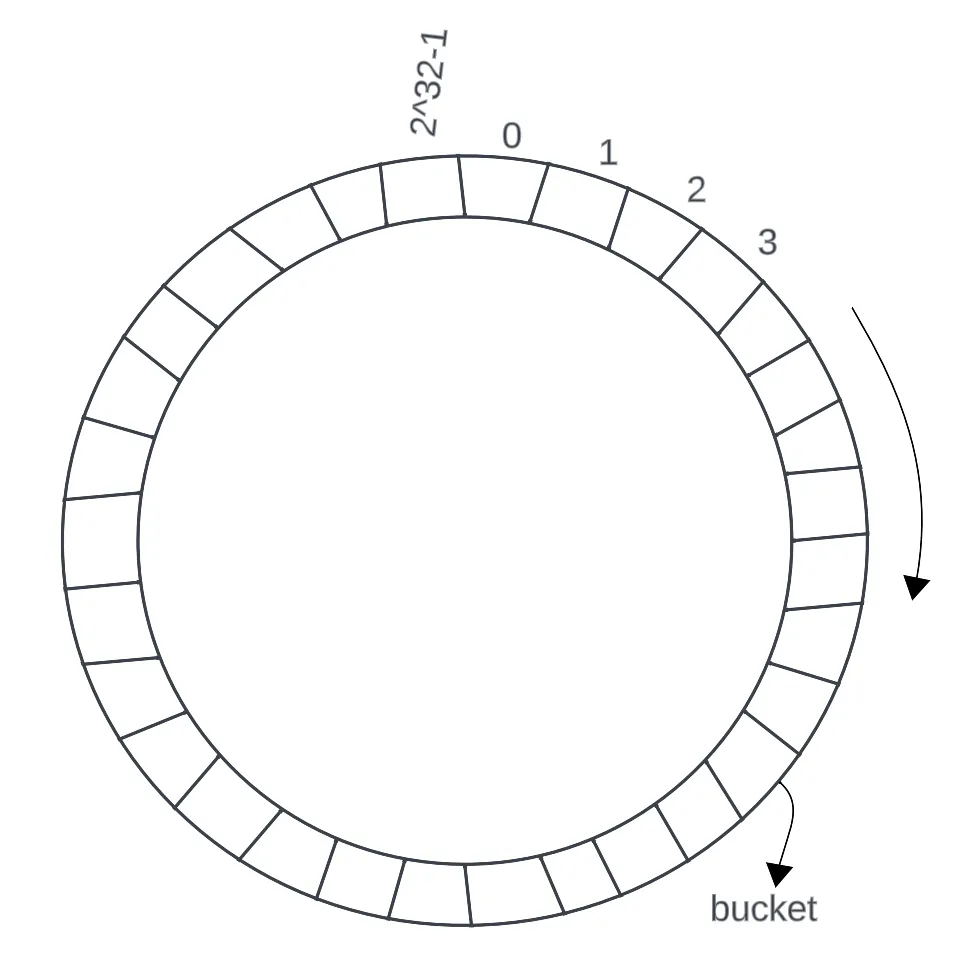
然后,将 服务器节点 通过 哈希函数 映射到环上的某个位置:
hash(S1) → 环上的一个点
hash(S2) → 环上的另一个点
...
同样,每个 key 也会被哈希映射到环上的某个点:
hash(key)
- 数据的分配规则
数据的放置:
从 key 的位置开始,顺时针找到第一个服务器节点,该服务器就是 key 的归属节点。 例如, 如果 key1 的哈希值在 S2 和 S3 之间,那么它会被分配给 S3。
节点变化时的稳定性
假设我们从 4 台服务器中移除 S3:
- 在传统哈希中,所有数据都要重新计算位置;
- 在一致性哈希中,只有原来属于 S3 的那部分数据需要重新分配,其他数据保持不变。
同理,当新增一个节点时,只会影响环上相邻区域的一部分数据。
这种 “局部性” 是 “一致性哈希” 的关键所在。
负载不均衡问题与虚拟节点
由于节点的哈希位置是随机分布的,可能出现某个服务器负责的数据量明显多于其他节点的情况。
为了解决这个问题,引入了虚拟节点(Virtual Nodes):
- 每个物理服务器对应多个虚拟节点;
- 每个虚拟节点在环上占据不同的位置;
- 数据仍然按哈希值映射到最近的虚拟节点;
- 最终将虚拟节点再映射回对应的物理服务器。
这样可以显著提高负载均衡效果。
一致性哈希的优点
高可扩展性: 节点的增加或移除只影响部分数据迁移。
高容错性: 某台服务器宕机后,只有它负责的数据需要重新分配。
易于分布式实现: 无需全局重算,节点独立工作即可。
负载均衡: 结合虚拟节点后,数据分布更加均匀。
典型应用场景
- 分布式缓存
在分布式缓存中,一致性哈希用于将 key 分配到不同的缓存节点中。
当节点增删时,不会导致整个缓存失效,只需迁移少量数据。
- 分布式存储系统(Cassandra, Dynamo)
在分布式数据库中,每个节点只负责环上部分哈希区间的数据。
一致性哈希使得系统具备天然的可扩展性和高可用性。
- 负载均衡与代理路由
例如 Nginx 或反向代理系统,可以使用一致性哈希来将相同的用户请求始终路由到同一台服务器,保证 session 一致性。
代码示例
以下是一个简单的 Python 实现:
import hashlib
from bisect import bisect_right
from typing import List, Optional
class ConsistentHash:
"""一致性哈希实现
特点:
- 使用虚拟节点提高分布均匀性
- 支持动态添加/删除节点
- 最小化节点变动时的数据迁移
"""
def __init__(self, nodes: Optional[List[str]] = None, virtual_nodes: int = 150):
"""初始化一致性哈希环
Args:
nodes: 初始节点列表
virtual_nodes: 每个物理节点对应的虚拟节点数量
"""
self.virtual_nodes = virtual_nodes
self.ring = {} # 哈希环: {hash_value: node_name}
self.sorted_keys = [] # 排序的哈希值列表
self.nodes = set() # 物理节点集合
if nodes:
for node in nodes:
self.add_node(node)
def _hash(self, key: str) -> int:
"""计算哈希值
使用MD5哈希并转换为整数
"""
return int(hashlib.md5(key.encode('utf-8')).hexdigest(), 16)
def add_node(self, node: str) -> None:
"""添加节点到哈希环
Args:
node: 节点名称
"""
if node in self.nodes:
return
self.nodes.add(node)
# 为每个物理节点创建多个虚拟节点
for i in range(self.virtual_nodes):
virtual_key = f"{node}#{i}"
hash_value = self._hash(virtual_key)
self.ring[hash_value] = node
self.sorted_keys.append(hash_value)
# 保持哈希值有序
self.sorted_keys.sort()
def remove_node(self, node: str) -> None:
"""从哈希环移除节点
Args:
node: 节点名称
"""
if node not in self.nodes:
return
self.nodes.remove(node)
# 移除该节点的所有虚拟节点
for i in range(self.virtual_nodes):
virtual_key = f"{node}#{i}"
hash_value = self._hash(virtual_key)
if hash_value in self.ring:
del self.ring[hash_value]
self.sorted_keys.remove(hash_value)
def get_node(self, key: str) -> Optional[str]:
"""获取key应该分配到的节点
Args:
key: 要查询的键
Returns:
节点名称,如果没有节点则返回None
"""
if not self.ring:
return None
hash_value = self._hash(key)
# 使用二分查找找到第一个大于等于hash_value的位置
index = bisect_right(self.sorted_keys, hash_value)
# 如果超出范围,则返回第一个节点(环形结构)
if index == len(self.sorted_keys):
index = 0
return self.ring[self.sorted_keys[index]]
def get_nodes_distribution(self, keys: List[str]) -> dict:
"""获取一组key在各节点的分布情况
Args:
keys: 键列表
Returns:
节点分布字典: {node_name: key_count}
"""
distribution = {node: 0 for node in self.nodes}
for key in keys:
node = self.get_node(key)
if node:
distribution[node] += 1
return distribution
def __repr__(self) -> str:
return f"ConsistentHash(nodes={len(self.nodes)}, virtual_nodes={self.virtual_nodes})"
# 使用示例
if __name__ == "__main__":
# 创建一致性哈希环
ch = ConsistentHash(nodes=["server1", "server2", "server3"], virtual_nodes=150)
print("=== 初始状态 ===")
print(f"哈希环: {ch}")
print(f"物理节点: {ch.nodes}")
# 测试key分配
test_keys = [f"key_{i}" for i in range(20)]
print("\n=== Key分配情况 ===")
for key in test_keys[:5]: # 只显示前5个
node = ch.get_node(key)
print(f"{key} -> {node}")
# 查看分布情况
print("\n=== 节点负载分布 ===")
distribution = ch.get_nodes_distribution(test_keys)
for node, count in sorted(distribution.items()):
print(f"{node}: {count} keys ({count / len(test_keys) * 100:.1f}%)")
# 添加新节点
print("\n=== 添加新节点 server4 ===")
ch.add_node("server4")
# 查看新的分布
new_distribution = ch.get_nodes_distribution(test_keys)
for node, count in sorted(new_distribution.items()):
print(f"{node}: {count} keys ({count / len(test_keys) * 100:.1f}%)")
# 计算数据迁移量
moved_keys = sum(abs(distribution.get(node, 0) - new_distribution.get(node, 0))
for node in ch.nodes) // 2
print(f"\n需要迁移的key数量: {moved_keys}/{len(test_keys)} ({moved_keys / len(test_keys) * 100:.1f}%)")
# 移除节点
print("\n=== 移除节点 server2 ===")
ch.remove_node("server2")
final_distribution = ch.get_nodes_distribution(test_keys)
for node, count in sorted(final_distribution.items()):
if node != "server2":
print(f"{node}: {count} keys ({count / len(test_keys) * 100:.1f}%)")
运行结果:
=== 初始状态 ===
哈希环: ConsistentHash(nodes=3, virtual_nodes=150)
物理节点: {'server3', 'server1', 'server2'}
=== Key分配情况 ===
key_0 -> server3
key_1 -> server3
key_2 -> server1
key_3 -> server1
key_4 -> server2
=== 节点负载分布 ===
server1: 9 keys (45.0%)
server2: 5 keys (25.0%)
server3: 6 keys (30.0%)
=== 添加新节点 server4 ===
server1: 7 keys (35.0%)
server2: 3 keys (15.0%)
server3: 5 keys (25.0%)
server4: 5 keys (25.0%)
需要迁移的key数量: 5/20 (25.0%)
=== 移除节点 server2 ===
server1: 9 keys (45.0%)
server3: 5 keys (25.0%)
server4: 6 keys (30.0%)
参考资料